Drawing Vertex based shapes using (r, theta) coordinates

This activity has the following desired goals:

• Learning to draw shapes using vertices at (r, theta) cordinates (A, M).
• Learning to draw curves using vertices at (r, theta) cordinates (A, M).
• Using the above ideas to make interesting curved figures (M, T).

Step 1

Type in the following code and run it:

clear()
showAxes()
showGrid()

def diagonal(x: Double, y: Double) = {
    math.sqrt(x * x + y * y)
}

val r1 = diagonal(50, 50)
val r2 = diagonal(100, 50)
val angle2 = math.atan2(50, 100).toDegrees
val r3 = diagonal(100, 100)

beginShape()
vertexRt(r1, 45)
vertexRt(r2, angle2)
vertexRt(r3, 45)
endShape()

Q1a. How does the above code differ from the Step 1 code in the previous lesson?

Q1b. What does the vertexRt(r, theta) command do?

Step 2

Type in the following code and run it:

clear()
setSpeed(fast)
showAxes()
showGrid()

beginShape()
curveVertexRt(150, 0)
curveVertexRt(150, 0)
curveVertexRt(150, 90)
curveVertexRt(150, 180)
curveVertexRt(150, 180)
endShape()
invisible()

Q2a. Read through the code above and try to understand what it does. What does the above code do? How does it do it?

Q2b. What does the curveVertexRt(r, theta) command do?

Q2c. How many curveVertexRt(r, theta) calls are required to make a curve?

Q2d. Do the first and last curveVertexRt(r, theta) calls play a special role in defining the curve to be made?

Explanation

Command Descriptions:

• beginShape() - begins a shape made out of vertices.
• vertexRt(r, theta) - adds a vertex to the current shape at the given (r, theta) location.
• curveVertexRt(r, theta) - adds a curve vertex to the current shape at the given (r, theta) location.
• endShape() - finishes the current shape and draws it out.

Exercise

1 Write a program to make the following figure using two different (beginShape plus curveVertexRts plus endShape) shapes:

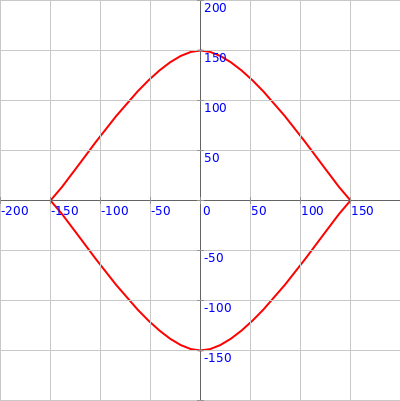
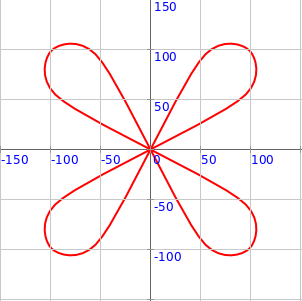
2 Write a program to make the following figure using four different (beginShape plus curveVertexRts plus endShape) shapes: