Mandala Building Blocks - 1
This activity has the following desired goals:
- Learning about the different pre-defined mandala building blocks (A, M).
- Building Block 1 - Lotus Petal
- Building Block 2 - Diya
- Building Block 3 - Pointed Petal
- Building Block 4 - Rounded Petal
Building Block 1 - Lotus Petal
Type in the following code and run it:
def lotusPetal(radius: Double, radiusOuter: Double,
theta: Double, thetaExtent: Double) = Picture.fromVertexShape { s =>
import s._
val tDelta = thetaExtent / 2
beginShape()
curveVertexRt(radius, theta - tDelta)
curveVertexRt(radius, theta - tDelta)
val rExtent = radiusOuter / radius
curveVertexRt(mathx.lerp(radius, radius * rExtent, 0.6), theta - tDelta * 22 / 30)
curveVertexRt(mathx.lerp(radius, radius * rExtent, 0.7), theta - tDelta * 2 / 30)
curveVertexRt(radius * rExtent, theta)
curveVertexRt(mathx.lerp(radius, radius * rExtent, 0.7), theta + tDelta * 2 / 30)
curveVertexRt(mathx.lerp(radius, radius * rExtent, 0.6), theta + tDelta * 22 / 30)
curveVertexRt(radius, theta + tDelta)
curveVertexRt(radius, theta + tDelta)
endShape()
}
cleari()
showAxes()
showGrid()
val pic = lotusPetal(150, 200, 0, 60)
draw(pic)

Q1a. The code above makes one lotus petal. What is its radius? What is its outer radius? What is its direction (theta)? What is it’s spread (thetaExtent)?
Exploration
Play with the inputs to the lotusPetal function above to make different kinds of petals.
Type in the following code and run it:
def lotusPetal(radius: Double, radiusOuter: Double,
theta: Double, thetaExtent: Double) = Picture.fromVertexShape { s =>
import s._
val tDelta = thetaExtent / 2
beginShape()
curveVertexRt(radius, theta - tDelta)
curveVertexRt(radius, theta - tDelta)
val rExtent = radiusOuter / radius
curveVertexRt(mathx.lerp(radius, radius * rExtent, 0.6), theta - tDelta * 22 / 30)
curveVertexRt(mathx.lerp(radius, radius * rExtent, 0.7), theta - tDelta * 2 / 30)
curveVertexRt(radius * rExtent, theta)
curveVertexRt(mathx.lerp(radius, radius * rExtent, 0.7), theta + tDelta * 2 / 30)
curveVertexRt(mathx.lerp(radius, radius * rExtent, 0.6), theta + tDelta * 22 / 30)
curveVertexRt(radius, theta + tDelta)
curveVertexRt(radius, theta + tDelta)
endShape()
}
cleari()
showAxes()
showGrid()
val pics = ArrayBuffer.empty[Picture]
repeatFor(0 to 6) { n =>
val pic = lotusPetal(150, 200, n * 60, 60)
pics.append(pic)
}
draw(pics)
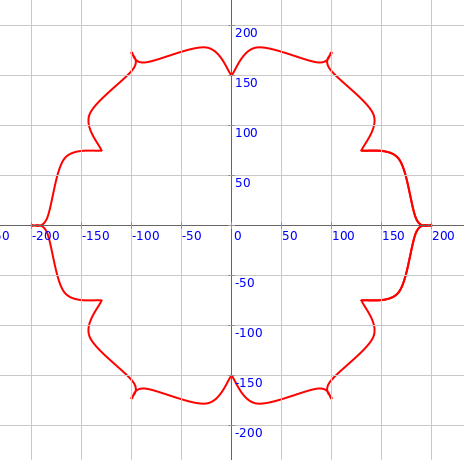
Q1b. How does the above code make lotus petals in a circular pattern?
Exploration
Play with the above code to make different kinds of circular patterns
Building Block 2 - Diya
Type in the following code and run it:
def diya(radius: Double, radiusOuter: Double,
theta: Double, thetaExtent: Double) = Picture.fromVertexShape { s =>
import s._
val tDelta = thetaExtent / 2
val rExtent = radiusOuter / radius
beginShape()
curveVertexRt(radius, theta)
curveVertexRt(radius, theta)
curveVertexRt(mathx.lerp(radius, radius * rExtent, 0.5), theta - tDelta / 4)
curveVertexRt(radius * rExtent, theta)
curveVertexRt(radius * rExtent, theta)
endShape()
beginShape()
curveVertexRt(radius * rExtent, theta)
curveVertexRt(radius * rExtent, theta)
curveVertexRt(mathx.lerp(radius, radius * rExtent, 0.5), theta + tDelta / 4)
curveVertexRt(radius, theta)
curveVertexRt(radius, theta)
endShape()
}
cleari()
showAxes()
showGrid()
val pic = diya(150, 250, 0, 50)
draw(pic)
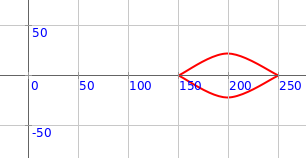
Q2a. The code above makes one diya. What is its radius? What is its outer radius? What is its direction (theta)? What is it’s spread (thetaExtent)?
Exploration
Play with the inputs to the diya function above to make different kinds of diyas.
Exercise
Make the following circular pattern:
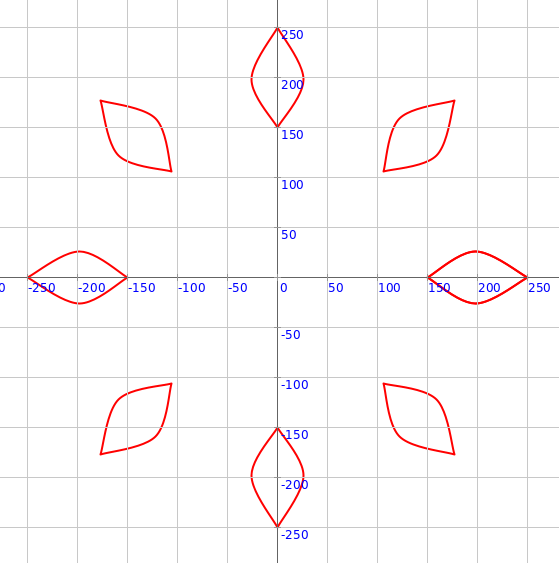
Building Block 3 - Pointed Petal
Type in the following code and run it:
def pointedPetal(radius: Double, radiusOuter: Double,
theta: Double, thetaExtent: Double) = Picture.fromVertexShape { s =>
val tDelta = thetaExtent / 2
import s._
beginShape()
curveVertexRt(radius, theta - tDelta)
curveVertexRt(radius, theta - tDelta)
curveVertexRt(radius + (radiusOuter - radius) / 2, theta - 2 * tDelta / 3)
curveVertexRt(radiusOuter, theta)
curveVertexRt(radius + (radiusOuter - radius) / 2, theta + 2 * tDelta / 3)
curveVertexRt(radius, theta + tDelta)
curveVertexRt(radius, theta + tDelta)
endShape()
}
cleari()
showAxes()
showGrid()
val pic = pointedPetal(150, 250, 0, 60)
draw(pic)
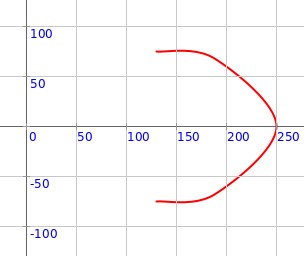
Q3a. The code above makes one pointed petal. What is its radius? What is its outer radius? What is its direction (theta)? What is it’s spread (thetaExtent)?
Exploration
Play with the inputs to the pointedPetal function above to make different kinds of petals.
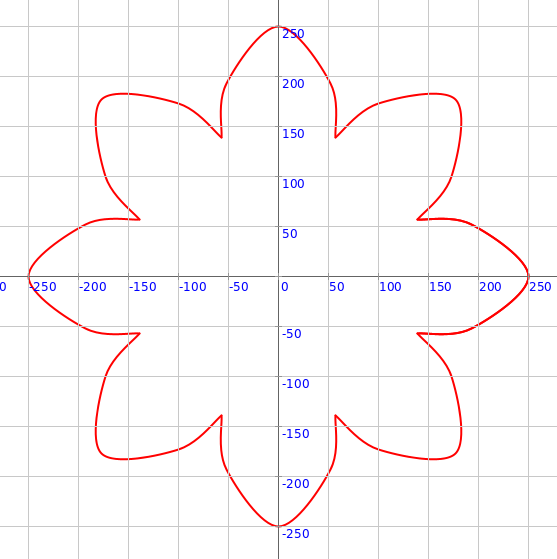
Exercise
Make the following circular pattern:
Building Block 4 - Rounded Petal
Type in the following code and run it:
def roundedPetal(radius: Double, radiusOuter: Double,
theta: Double, thetaExtent: Double) = Picture.fromVertexShape { s =>
val tDelta = thetaExtent / 2
import s._
implicit val s2 = s
beginShape()
curveVertexRt(radius, theta - tDelta)
curveVertexRt(radius, theta - tDelta)
curveVertexRt(radius + 3 * (radiusOuter - radius) / 4, theta - tDelta / 2)
curveVertexRt(radiusOuter, theta)
curveVertexRt(radius + 3 * (radiusOuter - radius) / 4, theta + tDelta / 2)
curveVertexRt(radius, theta + tDelta)
curveVertexRt(radius, theta + tDelta)
endShape()
}
cleari()
showAxes()
showGrid()
val pic = roundedPetal(150, 250, 0, 40)
draw(pic)
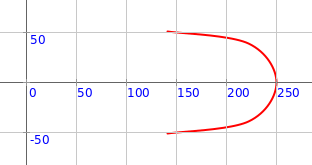
Q4a. The code above makes one rounded petal. What is its radius? What is its outer radius? What is its direction (theta)? What is it’s spread (thetaExtent)?
Exploration
Play with the inputs to the roundedPetal function above to make different kinds of petals.
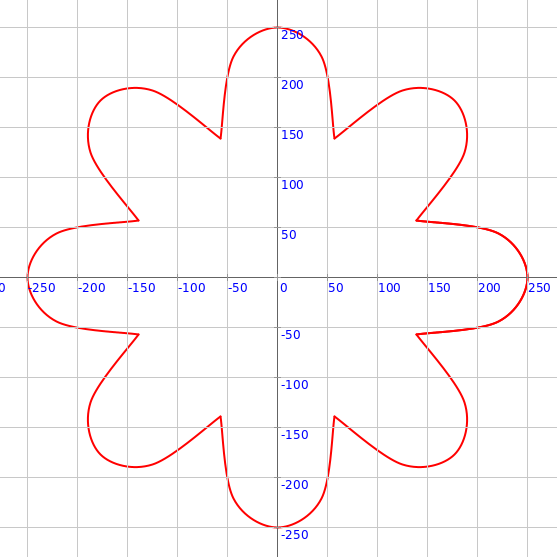
Exercise
Make the following circular pattern:
Copyright © 2010–2025 Kogics Foundation. Licensed as per Terms of Use.