Mandala Building Blocks - 2
This activity has the following desired goals:
- Learning about the different pre-defined mandala building blocks (A, M).
Building Block 5 - Semi Circular Petal
Type in the following code and run it:
def semiCircularPetal(radius: Double, theta: Double, thetaExtent: Double) = Picture.fromVertexShape { s =>
val tDelta = thetaExtent / 2
import s._
beginShape()
curveVertexRt(radius, theta - tDelta)
curveVertexRt(radius, theta - tDelta)
curveVertexRt(radius + (0.7010526 * thetaExtent), theta - tDelta / 2)
curveVertexRt(radius + (0.93333 * thetaExtent), theta)
curveVertexRt(radius + (0.7010526 * thetaExtent), theta + tDelta / 2)
curveVertexRt(radius, theta + tDelta)
curveVertexRt(radius, theta + tDelta)
endShape()
}
cleari()
showAxes()
showGrid()
val pic = semiCircularPetal(150, 0, 80)
draw(pic)
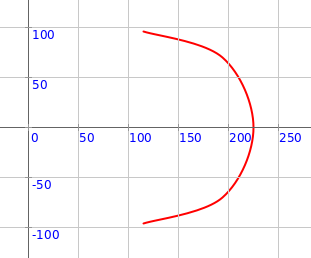
Q5a. The code above makes one semi circular petal. What is its radius? What is its direction (theta)? What is it’s spread (thetaExtent)?
Exploration
Play with the inputs to the semiCircularPetal function above to make different kinds of petals.
Exercise
Make the following circular pattern:

Building Block 6 - Inscribed Triangle
Type in the following code and run it:
def inscribedTriangle(vertexR: Double, vertexTheta: Double) = Picture.fromVertexShape { s =>
import s._
beginShape()
vertexRt(vertexR, vertexTheta)
vertexRt(vertexR, vertexTheta + 120)
vertexRt(vertexR, vertexTheta + 240)
vertexRt(vertexR, vertexTheta)
endShape()
}
cleari()
showAxes()
showGrid()
val pic = inscribedTriangle(150, 0)
draw(pic)

Q6a. The code above makes one inscribed triangle. What is its circumscribing radius? What is its direction (theta)?
Exploration
Play with the inputs to the inscribedTriangle function above to make different kinds of triangles.
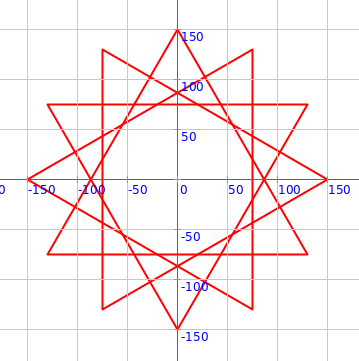
Exercise
Make the following circular pattern:
Building Block 7 - Inscribed Square
Type in the following code and run it:
def inscribedSquare(vertexR: Double, vertexTheta: Double) = Picture.fromVertexShape { s =>
import s._
beginShape()
vertexRt(vertexR, vertexTheta)
vertexRt(vertexR, vertexTheta + 90)
vertexRt(vertexR, vertexTheta + 180)
vertexRt(vertexR, vertexTheta + 270)
vertexRt(vertexR, vertexTheta)
endShape()
}
cleari()
showAxes()
showGrid()
val pic = inscribedSquare(150, 0)
draw(pic)
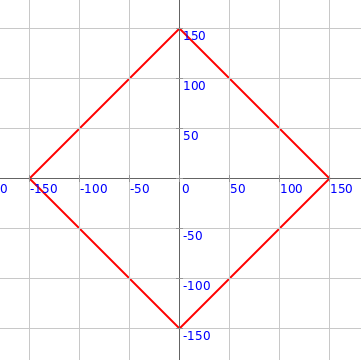
Q7a. The code above makes one inscribed square. What is its circumscribing radius? What is its direction (theta)?
Exploration
Play with the inputs to the inscribedSquare function above to make different kinds of squares.
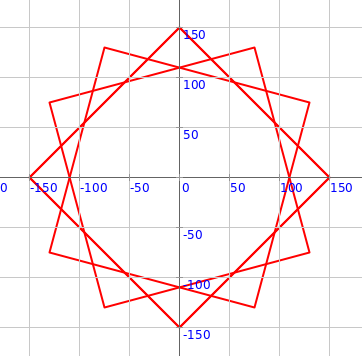
Exercise
Make the following circular pattern:
Building Block 8 - Altar
Type in the following code and run it:
def altar(r: Double, gateRFraction: Double, gateTheta: Double) = Picture {
setHeading(gateTheta)
hop(r)
left(90)
val glen = r * gateRFraction
hop(glen)
repeat(4) {
forward(r - glen)
left()
forward(r - glen)
right()
forward(r / 10)
right()
forward(r / 4)
left()
forward(r / 10)
left()
forward(r / 4)
forward(glen * 2)
forward(r / 4)
left()
forward(r / 10)
left()
forward(r / 4)
right()
forward(r / 10)
right(90)
}
}
cleari()
showAxes()
showGrid()
val pic = altar(200, 0.1, 0)
draw(pic)
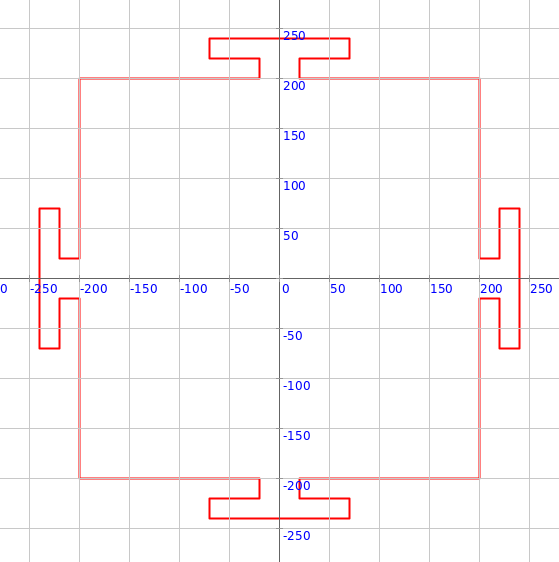
Q8a. The code above makes an altar. What is its inscribing radius? What is its direction (theta)?
Exploration
Play with the inputs to the altar function above to make different kinds of altars.
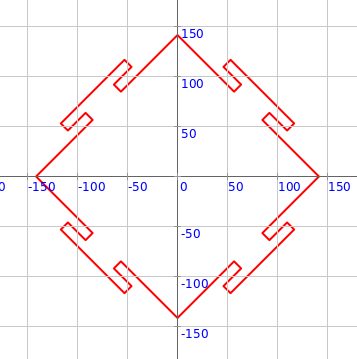
Exercise
Make the following circular pattern:
More building blocks coming soon…
Copyright © 2010–2025 Kogics Foundation. Licensed as per Terms of Use.